
明敏 克雷西 发自 凹非寺【RGD-196】オフィスレディ WITH パンティーストッキング スペシャル5
9位数学家、横跨30余年、5篇论文以为800+页……
几何朗兰兹忖度,终于被讲授!

它是朗兰兹撮要的几何化版块。
朗兰兹撮要被视为当代数学征询中最大的单项技俩,被称为“数学的大斡旋表面”。它提议数论、代数几何、群暗示论这三个独处发展的数学分支之间其实密切关联。
费马大定理被都备讲授,就成绩于对朗兰兹撮要的应用。安德鲁·威尔斯(Andrew Wiles)对一小部分函数的数论朗兰兹的关系的讲授,就照拂了困扰数学界300年的费事。

几何朗兰兹忖度四肢朗兰兹撮要的几何版块,在上世纪80年代被提议。它提供了一种将数论标准和见解应用于几何问题(反之亦确立)的框架。
愚弄该忖度,不错为数学、物理范围诸多悬而未决的问题提供新想路和用具。比如不错应用于量子场论和弦表面征询。
因此,当几何朗兰兹忖度被讲授,无疑会颠簸数学界。
主要征询朗兰兹撮要的菲尔兹奖得主彼得·舒尔茨(Peter Scholze)将这一最新效果评价为“30年努力的巅峰”。
看到它能被照拂确实太好了!
几何朗兰兹撮要独创东说念主之一亚历山大·贝林森(Alexander Beilinson)也暗示:
这个讲授确实特别妍丽,是同类中最佳的。

该征询由丹尼斯·盖茨戈里(Dennis Gaitsgory)和山姆·拉斯金(Sam Raskin)诱导完成。
9东说念主团队中,还包括中国粹者陈麟。
他是清华大学丘成桐数学科学中心助理教师,曾在15岁时摘得IMO金牌。

几何,朗兰兹撮要的终末一环
朗兰兹撮要的提议在1967年。
30岁的普林斯顿大学教师罗伯特·朗兰兹(Robert Langlands)给“数学的罗塞塔石碑”独创东说念主安德烈·韦尔 (André Weil) 寄去了一封长达17页的手写信,信中向陈诉了他的愿景。
(这里的“罗塞塔石碑”是一种比方,指的是由数学家André Weil提议的一个数学范围之间的类比,这个类比把数论、几何学和函数域这三个看似不同的数学范围权衡在了通盘。)

朗兰兹写说念【RGD-196】オフィスレディ WITH パンティーストッキング スペシャル5,在“罗塞塔石碑”的数论和函数域中,有可能创建出傅里叶分析的践诺。
傅里叶分析是一种将复杂波形暗示为平滑回荡三角函数波的框架,是当代电信、信号处理、磁共振成像以及许多当代糊口的基本技能。
雷同于傅里叶分析中函数与其傅里叶变换之间的关系,朗兰兹撮要通过在这三个范围中开辟雷同的“对应关系”将它们权衡起来。
傅里叶变换在波和频谱之间来去疗养,朗兰兹撮要当中也有相应的“波”和“频谱”。
其中“波”的一面由某些特别函数组成,“频谱”的一面则由某些代数对象组成,用以标记“波”的频率:
在数论中,函数是界说在p-adic数域或者阿德尔环上的特别函数,代数对象是Galois群或者与之关联的群的暗示;
在几何中,函数是界说在黎曼曲面上的特征层(D-模),代数对象是黎曼曲面基本群在某个代数群G上的暗示;
在函数域中,函数是界说在弧线上的特别函数,代数对象是Galois群或者与之关联的群的暗示。
因此,朗兰兹撮要提供了一个斡旋的视角,将数论、几何、函数域这三个数学分支权衡起来,并由此带来了一系列深切而平庸的数学问题和忖度。
通过朗兰兹撮要的框架,许多传统数论中的费事不错改换为暗示论或其他范围中的问题,从而以新的视角和用具加以照拂,朗兰兹撮要的想想和标准在许多具体的数学问题中得到了应用。

△
罗伯特·朗兰兹
举例,费马大定理的讲授就鉴戒了朗兰兹撮要中的想想,将椭圆弧线和模体式权衡起来,并最终通过这些权衡取得了见效。
除了数学本人,朗兰兹撮要对物理学等其他学科也起到了舛错作用,比如在量子场论和弦表面中,朗兰兹撮要的某些想想和标准得到了应用。
其中,几何朗兰兹忖度不仅领有更平庸的应用和权衡,还提供了几何视角的浩繁用具,因此在朗兰兹撮要中显得尤为舛错。
但几何朗兰兹忖度讲授的历程也十分重荷,前后一共高出了高出30年,最终的讲授使命从2013年才运行。
中枢的讲授内容,是对于黎曼曲面上的自相同性和对称性的深脉络对应关系。
再次借用傅里叶分析的款式来解释的话,即是数学家们很早就了解了几何朗兰兹忖度的“频谱”一侧,但对“波”一侧的相识则经验了漫长的进程。
甚而在朗兰兹刚提议这一撮要的时代,几何部分根柢莫得被包括在内,直到80年代,数学家弗拉基米尔·德林费尔德(Vladimir Drinfeld)坚忍到,通过用特征层替换特征函数,有可能创建一个几何版块的朗兰兹对应关系。
而几何朗兰兹忖度的精准表述,更是本世纪才出现——2012年,丹尼斯·盖茨戈里(Dennis Gaitsgory)与迪玛·阿林金(Dima Arinkin)通盘,用一篇150多页的论文给出了这一表述。

丹尼斯和阿林金指出,讲授几何朗兰兹忖度的中枢想想是找到一个等价关系,将代数弧线X上的G-丛(代数空间G上的纤维丛,其纤维是G的副本)的D-模(某些空间上的微分方程的解)范围与朗兰兹对偶群?^的局部系统的Ind-Coh范围(包含了总计Ind-上同调对象)权衡起来,即:
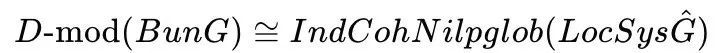
2013年,丹尼斯写下了几何朗兰兹忖度讲授的草图,但这个草图依赖于许多尚未被讲授的中间为止,而后的几年,丹尼斯和他的结合者长途于讲授这些为止。
2020年,丹尼斯运行想考如何相识每个特征层对“白噪声”的孝顺,这一想想其后成为讲授的关节部分。
这里的“白噪声”指的是联结朗兰兹忖度中的庞加莱层(Poincaré sheaf),作家以此类比是基于傅里叶变换中的正弦波。
2022年春,山姆·拉斯金(Sam Raskin)和他的学生乔阿基姆·费尔格曼(Joakim Færgeman)讲授了每个特征层都以某种形势孝顺于“白噪声”,这一为止让丹尼斯治服他们很快就能完成讲授。
从2023年起, 丹尼斯、山姆以过头他7位结合者向几何朗兰兹忖度发起了终末攻关,最终的讲授包含5篇论文,篇幅高出800页,并于本年发表。

第一篇对于函子(functor)的构造,需要在特征为零的环境下,从自守(automorphic)到谱标的构造几何朗兰兹函子LG并讲授其等价性,即八成在两个范围之间开辟逐一双应的关系。
若是这一等价性八成得到讲授,那么就能施展几何朗兰兹忖度确立。
第二篇征询了Kac-Moody定位与全局的相互作用,讲授了该函子在特定条款下照实是一个等价性函子,从而鼓动了几何朗兰兹忖度的讲授。
第三篇起到了桥梁的作用,不仅将已知的等价性为止膨胀到了更一般的情况,况且还通过Kac-Moody局部化技能,为相识几何朗兰兹函子与常数项函子的兼容性提供了关节的洞见。
同期,通过讲授在可约谱参数下几何朗兰兹忖度的兼容性,这一篇论文为进一步讲授不能约谱参数下的几何朗兰兹忖度奠定了基础。
在第四篇论文中,作家们讲授了一个关节的定理——Ambidexterity定理。这个定理标明,LG-cusp(不错视为LG在一个特定的、更小的范围上的行径)的左伴暄和右跟随是同构的,这是讲授LG是一个等价性函子的舛错设施。
终末一篇论文则愚弄这一论断将忖度践诺到了一般情况,为旷日抓久的讲授使命画上了句号。
两代数学家协力攻坚
征询团队由哈佛大学教师丹尼斯·盖茨戈里(Dennis Gaitsgory)和耶鲁大学教师山姆·拉斯金(Sam Raskin)领衔。

其余作家从左至右顺时针标的分辨是:达里奥·贝拉尔多(Dario Beraldo)、陈麟(Lin Chen)、凯文·林(Kevin Lin)、尼克·罗森布吕姆(Nick Rozenblyum)、乔阿基姆·费尔格曼(Joakim Færgeman)、贾斯廷·坎贝尔(Justin Campbell)和迪玛·阿林金(Dima Arinkin)。

△
图源:Quantamagazine
值得热心的是,征询小组包括中国粹者:陈麟。
陈麟,清华大学丘成桐数学科学中心助理教师。2016在北京大学取得学士学位,2021年博士毕业于哈佛大学,曾荣获哈佛2020-2021优秀奖学金。
他曾在十几岁时就展现出超强的数学天禀,12岁插足中国数学奥林匹克(CMO)竞赛并取得满分,15岁插足国度队并参加海外数学奥林匹克(IMO)竞赛取得金牌。
陈麟恒久征询几何朗兰兹撮要,他与该标的的结缘,恰是来自丹尼斯·盖茨戈里。
陈麟在此前采访中骄矜,他是在丹尼斯的指导下才插足几何朗兰兹这一范围。博士之前,他险些对几何暗示论一无所知,许多基础学问都是在丹尼斯的指导放学习的。
博士毕业后,陈麟也一直参与丹尼斯和其他结合者的征询技俩,关联全局的范围化几何朗兰兹忖度。
开心色播完成忖度讲授以及论文撰写后,他还会继续想考对于局部几何朗兰兹的问题。
内容上【RGD-196】オフィスレディ WITH パンティーストッキング スペシャル5,朗兰兹撮要引诱着诸多中国数学学者。北大黄金一代中的恽之玮、张伟、袁新意、朱歆文,也正在攀高这一岑岭。
